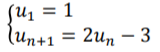Chapter 2 - Programming Variables, assignment and display 12
Loops 16
Tests 17
2 and 3D plots 18
Supplements on matrices and vectors 23
Calculation accuracy 29
Solving differential equations 30
ในตัวอย่างที่ให้มาในเอกสารนี้ แต่ละบรรทัดจะนำหน้าด้วย “ --> “ คือคำสั่ง บรรทัดอื่นคือส่วนที่ได้จากคำสั่ง (ผลการคำนวณ, รายงานข้อผิดพลาด) ไม่ต้องเขียน “ --> “ ในเอดิเตอร์ . ที่จะเริ่มต้นตอนนี้ที่ชี้ให้เห็นถึงความแตกต่างระหว่างบรรทัดคำสั่งและผลการคำนวณตามที่แสดงให้เห็นในคอนโซลหลังจากสำเนาและนำไปวาง เมื่อนำเสนอในรูปตารางหนึ่ง (โดยปราศยาก “ --> “ และไม่แสดงผลการคำนวณ) คำสั่งถูกกำหนดชัดเจน เหมือนที่ควรจะพิมพ์ไว้ในเอดิเตอร์ ตัวแปร การกำหนดค่า และการแสดงตัวแปรไซแลบไม่ใช่ระบบพีชคณิตคอมพิวเตอร์ การคำนวณเฉพาะกับจำนวณตัวเลข การคำนวณทั้งหมดสำเร็จลงได้ด้วยเมทริกซ์ แม้ว่าการดำเนินการนี้ไม่อาจสังเกตได้ แม้ว่ามโนทัศนฺ์ของเมทริกซ์ไม่เป็นที่รู้จัก เวคเตอร์ และ แถวลำดับ (sequences) ของจำนวนสามารถจะอธิบายได้ตามที่เป็น จริงแล้วเมทริกซ์ของ 1xn มิติ หรือ nx1 และจำนวนหนึ่งๆโดยตัวเองเป็นเมตริกซ์มิติ 1 × 1. ตัวแปรไม่จำเป็นต้องประกาศไว้ก่อนล่วงหน้า แต่ตัวแปรใดๆต้องมีค่าค่าหนึ่ง ตัวอย่างเช่น การให้ได้มาค่าของตัวแปรหนึ่ง ซ่ึ่งยังไม่ได้กำหนดค่ามาก่อนก่อให้เกิดข้อผิดพลาด
-->a !--error 4 Undefined variable : a
ถ้ามีค่าหนึ่งถูกกำหนดให้ตัวแปรหนึ่ง ก็จะไม่มีข้อผิดพลาดอีกต่อไป
--> a=%pi/4
a = 0.7853982
--> a
a = 0.7853982
ตัวแปรอาจเป็นชื่อใดชื่อหนึ่งได้ที่ไม่ได้กำหนดไว้ก่อนโดยระบบ
--> Piby2=%pi/2
Piby2 = 1.5707963
กล่าวถึงคล้ายกับฟังก์ชันไซแลบ ชื่อตัวแปรหนึ่งๆจะต้องมีตัวอักขระหรืออักขระพิเศษ
ผลการคำนวณที่ไม่ได้กำหนดให้ตัวแปร จะกำหนดให้ตัวแปรที่เรียกว่า ans: โดยอัตโนมัติ
-->3*(4-2)
ans = 6.
-->ans
ans = 6.
ฟังก์ชัน(Functions)
ฟังก์ชันเป็นแนวทางที่เป็นธรรมชาติง่ายที่สุดที่จะคำนวณจากตัวแปร และให้ได้ผลลัพธ์จากตัวแปร.
นิยามของฟังก์ชันหนึ่งเริ่มต้นด้วย function และจบด้วย endfunction ตัวอย่างเช่นในการแปลง euros(e) ให้ได้คำตอบเป็นดอลล่าdollars (d) ด้วยอัตราการแลกเปลี่ยน exchange rate (t), โดยกำหนดdollars function ตัวแปรที่มีคือ e และ t และ image คือ d
-->function d=dollars(e,t);
d=e*t; endfunction
-->dollars(200,1.4) ans = 280.
ตามปกติแล้วฟังก์ชันเชิงจำนวนหรือตัวเลข เป็นฟังก์ชันของตัวแปรจริงหนึ่ง ตัวอย่างเช่น ฟังก์ชัน f และ ฟังก์ชัน g ถูกกำหนดโดยใช้คำสั่งต่อไปนี้
-->function y=f(x); y=36/(8+exp(-x)); endfunction
-->function y=g(x); y=4*x/9+4; endfunction
การกำหนดฟังก์ชันแล้วสามารถใช้เพื่อคำนวณหาค่าดังนี้
--> f(10) ans = 4.4999745
--> g(12.5) ans = 9.5555556
การกำหนดค่าให้ตัวตัวแปรหนึ่ง (requesting the assignment of a variable)
การกำหนดค่าให้ตัวแปรทำใด้ง่ายโดยการใช้เครื่องหมายกระทำ “ = “
Display
Writing
เพียงแต่พิมพ์ชื่อของตัวแปรหนึ่งๆ ก็จะแสดงผลค่าของตัวแปรนั้น นอกจากว่ามีเครื่องหมายเซมิโคลอน “ ; “ อยู่ตอนท้ายของบรรทัดคำสั่ง
Brackets
เมทริกซ์ถูกกำหนดขึ้นโดยใช้วงเล็บเหลี่ยม (square brackets). ตามที่กล่าวถึงมาก่อนแล้ว การคำนวณเมทริกซ์ เป็นรากฐานของการคำนวณในไซแลบ ช่่องว่าง หรือ คอมม่าใช้ในการแยกคอร์ลัมน์ และเซมิโคลอนใช้ในการแยกแถว เพื่อที่จะกำหนดเวคเตอร์คอร์ลัม และให้ผลการแสดงเป็นคอร์ลัมดังนี:
-->v=[3;-2;5]
v =
3.
- 2.
5.
เพื่อกำหนดเวคเตอร์แถว และให้แสดงผลแถวของเมทริกซ์ดังนี้
-->v=[3,-2,5]
v =
3. - 2. 5.
หมายเหตุ คำสั่งนี้สามารถพิมพ์ออกมาภายใต้รูปแบบ v=[3 -2 5] เพียงเว้นช่องว่างระหว่างสมาชิกในวงเล็บ
เพื่อที่จะกำหนดเมทริกซ์และให้แสดงผลแบบในแนวตั้ง หรือ แท่ง (tabular display)
-->m=[1 2 3;4 5 6;7 8 9]
m =
1. 2. 3.
4. 5. 6.
7. 8. 9.
หมายเหตุ คำสั่งนี้สามารถพิมพ์ออกมาภายใต้รูปแบบ m=[1,2,3;4,5,6;7,8,9]
ฟังก์ชัน disp
disp ต้องใช้ร่วมกับวงเล็บเสมอ กับเวคเตอร์ v ที่กำหนดไว้ก่อนหน้านี้
-->v(2)
ans =
- 2. -->
disp(v(2)) - 2.
เพื่อแสดงผลสตริง(มักอยู่ในรูปประโยค) ให้นำข้อความหรือสตริงที่ต้องการแสดงอยู่ในเครื่องหมายคำพูด
-->disp("Bob won")
Bob won
เพื่อแสดงผลการควบรวมของคำและค่าต่างโดยใช้คำสั่งสตริง ซึ่งแปลงค่าไปเป็นสตริงตัวอักขระ โดยการใช้เครื่องหมายบวก “ + “ ระหว่างส่วนที่แตกต่างกัน
-->d=500;
-->disp("Bob won "+string(d)+" dollars")
Bob won 500 dollars
ถ้าประโยคประกอบด้วยเครื่องหมายคำพูดเดี่ยว (single quote) การแสดงแบบแรกจำต้องใช้การซ้ำสองในสตริงที่ต้องการแสดงให้ถูกตำแหน่ง
-->disp("It''s fair")
It's fair
การเพิ่มที่ละสเต็บในลูป (Loops Incrementation)
ตัวกระทำโคลอน “ : “ ใช้ในการกำหนดเวคเตอร์ของจำนวน ที่ซึ่งประสานลำดับแบบเลขคณิต โดยให้เครื่องหมาย << สำหรับค่าเริ่มต้น : สเต็ป : ค่าปลายด้วยเครื่องหมาย>> (beginning value<<: ending="" step:="" value="">>. เป็นไปได้ที่ไม่เข้าสู่ค่าปลายหรือท้าย ถ้าไม่ระบุสเต็บที่เพิ่มหรือลด โดยมีค่าปริยายคือ 1
ตัวอย่างเช่น เพื่อกำหนดเวคเตอร์แถวของเลขจำนวนเต็ม ซึ่งการเพิ่มขึ้นสเต็บละ 1 จาก 3 และ 10
-->3:10
ans =
3. 4. 5. 6. 7. 8. 9. 10. or
ซึ่งการเพิ่มขึ้นสเต็ปละ 2 จาก 1 ถึง 10 ดังนี้
-->1:2:10
ans =
1. 3. 5. 7. 9.
หรือเป็นไปในทางที่ลดลงทีละสเต็ปของ 4 จาก 20 to 2:
-->u=20:-4:2
u = 20. 16. 12. 8. 4.
for
สำหรับโครงสร้างลูปที่ง่ายที่สุดสำหรับจำนวนที่ตายตัวของการทำงานซ้ำ เขียนได้เป็น for … end.
ตัวอย่าง: ให้คำนวณ 20 เทอมของลำดับที่กำหนดโดยการเกิดซ้ำตามความสัมพันธ์คือ
{u
1 = 4}
{u
n+1 = u
n + 2n +3}
Algorithm Scilab Editor
Put 4 in u(1) u(1)=4
For n from 1 to 20 for n=1 :20
u(n+1) takes the value u(n)+2n+3 u(n+1)= u(n)+2*n+3;
and u(n) display ([n,u(n)])
display n and u(n) end
End for
While
เพื่อหยุดลูปเมื่อกำหนดเป้าหมายที่จะไปถึง, โดยใช้ while … end
ฉันได้ปลูกต้นคริสมาสในปี 2005วัดได้สูง 1.20 m. ต้นไม้เติบโตขึ้นปีละ 30 ซม. ฉันตัดสินใจที่จะตัดต้นไม้นี้เมื่อมันสูงเกินกว่า 7 เมตร ในปีใดที่ฉันจะต้องตัดต้นไม้นี้
Algorithm Scilab Editor
Put 1.2 in h (h = tree height) h=1.2;
Put 2005 in y (y = year) y=2005;
While h<7 h="" nbsp="" p="" while=""> h takes the value h+0.3 (the tree grows) h=h+0.3;
y takes the value y+1 (one year passes) y=y+1;
End while end
Display y (the final year) disp("I will cut the.. tree in "+string(y))
หมายเหตุ เมื่อคำสั่งหนึ่งยาวเกินกว่าที่จะเขียนในบรรทัดเดียว เอดิเตอร์จะรวมบรรทัด สามารถทำได้โดยใช้สองจุด“ .. “ (two dots) ก่อนที่จะไปยังบรรทัดต่อไป
Tests
Comparison operators
การทดสอบที่มีประโยชน์รวมทั้งการเปรียบเทียบจำนวนหรือหาว่าประโยคคำสั่งใดเป็นจริงหรือเป็นเท็จ ข้างล่างนี้คำสั่งที่สอดคล้องกัน
Equal Different Less Greater Less or equal Greater or equal
== <> < > <= >=
True False And Or No
%T %F & | ~
หมายเหตุ จงระมัดระวังกับค่าความถูกต้องในการคำนวณ การคำนวณเป็นแนวทางเข้าสู่ และ “ == “ บางครั้งจะให้ผลลัพธ์ที่ผิดพลาด (ดูค่าความละเอียดใหนการคำนวณหน้า 30)
เพื่อเปรียบเทียบเวคเตอร์ 2 เวคเตอร์หรือ 2 เมทริกซ์ การทดสอบ “ == “ และ “ <> “ จะเปรียบเทียบเทอมต่อเทอม ตัวอย่างเช่น:
-->X=[1,2,5]; Y=[5,3,5];
-->X==Y
ans =
F F T
เพื่อทดสอบ 2 เวคเตอร์เท่ากันหรือไม่ ใช้ isequal และใช้ ~isequal ถ้า แตกต่างกัน
-->isequal(X,Y)
ans =
F
-->~isequal(X,Y)
ans =
T
If…then
ประโยคคำสั่งเงื่อนไขพื้นฐานดังต่อไปนี้
• if … then … else … end,
• if … then … elseif … then … else … end.
if … then ต้องเขียนอยู่บนบรรทัดเดียวกัน และเช่นเดียวกับ elseif … then.
ตัวอย่าง อลิษทอยลูกเต๋า 3 ลูก
• If she gets three 6’s she wins $20,
• If she gets three identical numbers different from 6 she wins $10,
• If she gets two identical numbers she wins $5,
• Otherwise she wins nothing.
ให้จำลองแบบการทดลองทอยลูกเต๋า และคำนวณการชนะรางวัลของอลิษโดยใช้ฟังก์ชัน
• grand (see page 22),
• unique(D)which keeps only once the values that appears several times in D,
• length(unique(D)) which returns the size of the obtained vector, that is to say 1 if three dice are equal, and 2 if two dice are equal.
Algorithm Scilab Editor
Put the three values in D D=grand(1,3,"uin",1,6);
If Alice gets three 6, then Alice wins 20 dollars if D==[6,6,6] then W=20;
Else if she receives three identical values, elseif length(unique(D))==1 then Alice wins 10 dollars hen W=10;
Else, if she receives two identical values, elseif length (unique(D))==2
then Alice wins 5 dollars then W=5;
Otherwise else
Alice wins nothing W=0;
End if end
Display Alice's winnings disp("Alice wins "+.. string(W)+ " dollars")
2-D and 3-D plots
คำสั่ง พล็อตใช้ในการพล็อตกราฟในระนาบ สีและการปรากฏให้เห็นสามารถระบุโดยการใช้ตัวบ่งชี้สีและรูปแบบจุดพล็อตภายในเครื่องหมายคำพูด
• Colors "b" = blue (by default), "k" = black, "r" = red, "g" = green, "c" = cyan, "m" = magenta, "y" = yellow, "w" = white.
• Point styles Joined (by default), or ".", "+", "o", "x", "*". Other options are available with: "s", "d", "v", "<", and ">".
การพล็อตกราฟพื้นฐาน (Basic plots)
การพล็อตจุดกราฟ
ให้พล็อตจุด A(1 ; 2) ด้วยจุดสีแดง
Scilab Editor Graphics Window
plot(1,2.".r")
 พล็อตเซ็กเมนต์(To plot a segment)
พล็อตเซ็กเมนต์(To plot a segment)
ให้พล็อตเซ็กเมนต์[AB] ด้วยสีฟ้า(่โดยปริยาย) ด้วย A(1 ; 2) และ B(3 ; 5).
Scilab Editor Graphics Window
plot([1,3],[2,5])

การพล็อตเคิร์ฟแนวราบโดยฟังก์ชัน y=f(x) (plot of plane curves by function y=f(x))
สำหรับฟังก์ชัน x → f(x) ค่าของ x ระบุไว้โดยใช้ คำสั่ง linspace โดยเขียนคำสั่งดังนี้ x=linspace(a,b,n); ซึ่ง a เป็นค่าน้อยที่สุดของตัวแปร x, b เป็นค่าสูงสุดของ x, และ n จำนวนค่าที่คำนวณระหว่างค่า a และ b อย่าลืมว่าสัญลักษณ์ “ ; “ นอกจากนี้แล้วทุกค่า n ของ x จะถูกนำออกมาแสดง
ตัวอย่างเช่น พิจารณาฟังก์ชัน 2 ฟังก์ชัน f และ g กำหนดอยู่ในช่วง [-2 ; 5] โดยที่:
f(x) = (x^2 + 2x)e^-x , และ and g(x) = sin x/2
ด้วยโปรแกรมข้างล่างนี้ ได้พล็อตเคิร์ฟกำหนดโดย f , สีฟ้าโดยปริยาย
Scilab Editor Graphics Window
function y=f(x)
y=(x^2+2*x)*exp(-x)
endfunction
x=linspace(-2,5,50);
plot(x,f)
โดยการเพิ่มโปรแกรมข้างล่าง จะได้การพล็อตของเส้นเคิร์ฟ 2 เส้น ที่เป็นของ f สีแดง และของ g สีเขียว
การพล็อตที่ผ่านมาล้างออกไปโดยใช้คำสั่ง clf(“ clear figure “).
Scilab Editor Graphics Window
function y=g(x)
y=sin(x/2)
endfunction
x=linspace(-2,5,50);
clf
plot(x,f,"r",x,g,"g")
พล็อตชุดของจุด(Plots of sequences of points)
Terms of a sequence
ในกรณีทั่วไปเกือบทั้งหมดจะพล็อตไปตามลำดับของจุด M(n,u(n)) หลังจากการคำนวณของพิกัดฉาก u(n) ของเวคเตอร์u.
plot(u,"*r") บ่งถึงสไตล์และสีของจุดในเครื่องหมายคำพูด สีแดงและรูดดาวที่ไม่เชื่อมต่อ โดยปริยายแล้วจุดต่างๆ ถูกพล็อตด้วยสีฟ้า และ เชื่อมต่อกัน
Scilab Editor Graphics Window
for n=1:50
u(n)=(-0.8)^n;
end clf;
plot(u,"*r")
ข้อมูลสถิติ 2 ตัวแปร (Bivariate statistical data)
ข้อมูลสถิติ 2 ตัวแปรถูกกำหนดขึ้นในรูปของเวคเตอร์ 2 เวคเตอร์ เรียกว่า X และ ํBivariate statistical data are given in the form of two vectors: let’s call them X and Y.
plot(X,Y,"<") พล็อตสแกตเตอร์กราฟของ M(Xi;Yi) (scatter plot of M(Xi;Yi) แสดงจุดพล็อตด้วยสามเหลี่ยมสีฟ้า
Scilab Editor Graphics Window
X=[1,3,3,7,7,9,10];
Y=[8,7,5,5,4,2,2];
clf; plot(X,Y,"<")
การพล็อตกราฟ 3 มิติ (Plots in 3 dimensions)
ไซแลบสามารถใช้ในการพล็อตพื้นผิว เคิร์ฟในสเปสซ์ ด้วยออพชันมากมายสำหรับจัดการผิวด้านที่ซ่อนบังไว้ สีของผิวหน้า, จุดในการมอง ฯลฯ ตัวอย่างต่อไปนี้แสดงการพล็อตกราฟ 3-D
ฟังก์ชัน surf สามารถใช้ในการพล็อตพื้นผิว ฟังก์ชันนี้มีตัวแปรนำเข้า 3 ตัวแปร x, y และ z. x และ y เป็นเว็คเตอร์ขนาดare respectively vectors of size m and n ตามลำดับ สอดคล้องกับจุดบนแกน(0x) และ(0y). z คือ เมทริกซ์ขนาดมิติ m×n ด้วยองค์ประกอบ z
ij สอดรับกับความสูงของจุดตามพิกัดX xi และพิกัดaY yi
เพื่อที่จะพล็อตพื้นผิวโดยฟังก์ชันในรูป z = f(x,y) ซึ่งต้องทำดังต่อไปนี้
• กำหนดฟังก์ชัน f
• คำนวณ z=feval(x,y,f)'
feval(x,y,f) คืนค่าเป็นreturns the m×n matrix ซึ่งองค์ประกอบ ij คือ f(xi,yi) ซึ่งจะถูกทรานสโพสโดยใช้เครื่องหมายคำพูดเดี่ยว“ ' “
• Execute surf(x,y,z).
เพื่อจะพล็อตพื้นผิว z = 2x^2 + y^2 (elliptic paraboloid):
Scilab Editor Graphics Window function
z=f(x,y)
z=2*x^2+y^2;
endfunction
x=linspace(-1,1,100);
y=linspace(-2,2,200);
z=feval(x,y,f)';
clf
surf(x,y,z)
เคิร์ฟในสเปสซ์อาจพล็อตโดยใช้ ฟังก์ชัน param3d โดยที่ param3d มี 3 อาร์กูเมนต์ x, y และ z, แต่ละเวคเตอร์มีมิติเดียวกัน และสอดคล้องกับจุด(xi,yi,zi) บนเคิร์ฟ
เพื่อพล็อต helix กำหนดโดยdefined by (x = cos t , y = sin t , z = t):
Scilab Editor Graphics Window
t=linspace(0,4*%pi,100);
param3d(cos(t),sin(t),t)
การจำลองแบบและสถิติ (Simulations and statistics)
มีหลายฟังก์ชันที่นำมาใช้ได้ในไซแลบเพื่อใช้ในการจำลองแบบได้เร็วและมีประสิทธิภาพ
ลำดับการสุ่ม (Random Sequences)
• grand(1,p,"uin",m,n) คืนกลับเป็นเวคเตอร์หนึ่ง ของ ลำดับการสุ่มจำนวนเต็ม p (p random integer sequences) ระหว่าง m และ n ด้วยจำนวนเต็มบวก p , m และ n เป็นจำนวนเต็มและ m ≤ n.
-->t = grand(1,4,"uin",1,6)
t =
3. 1. 3. 6.
• grand(1,p,"unf",a,b) คืนกลับค่าเป็นเว็คเตอร์หนึ่งของลำดับการสุ่มจำนวนจริงp (p random real sequences) ระหว่าง a และ b ด้วยจำนวนเต็มบวก , a และ b เป็นจำนวนจริง และ a ≤ b.
-->tr = grand(1,2,"unf",-1,1)
tr =
- 0.7460264 0.9377355
สถิติ (Statistics)
ฟังก์ชันมาตรฐานทางสถิติทั้งหมดแสดงรายการไว้ในหน้า 32
คิดไว้ในใจเป็นการเฉพาะกล่าวคือ
• ฟังก์ชัน bar(x,n,color) ซึ่งวาดกราฟแท่ง(bar graphs):
Scilab Editor Graphics Window
x=[1:10];
n=[8,6,13,10,6,4,16,7,8,5];
clf; bar(x,n)
• สำหรับกราฟแท่งที่แทน 2 ชุดด้านต่อด้าน(two sets side by side): พิจารณาชุดของค่า X และ 2 ชุดลำดับของจำนวน n1 และ n2. สำหรับการพล็อต n1 และ n2 ต้องเป็นเว็คเตอร์คอร์ลัมน์ นั่นคือทำไมจึงนำทรานสโพสมาใช้ในตัวอย่างข้างล่าง
Scilab Editor Graphics Window
X=[1,2,5];n1=[5,10,5];n2=[6,8,7];
bar(X,[n1',n2'])
อาร์กูเมนต์ทางเลือกสีกำหนดสีตามฟังก์ชันการพล็อต
ข่าวสารเพิ่มเติมของเมทริกซ์และเวคเตอร์ (Additional information on matrices and vectors)
การจัดการองค์ประกอบเว็คเตอร์
วงเล็บเหลี่ยมถูกนำมาใช้เพื่อกำหนดเมทริกซ์ สเปสซ์หนึ่งหรือคอร์ลัมน์หนึ่งๆถูกใช้เพื่อสลับจากคอร์ลัมน์หนึ่งไปเป็นอีกคอร์ลัมน์ และเซมิโคลอนถูกใช้เพื่อสลับจากบรรทัด(line)ไปเป็นอีกบรรทัด ดังนี้
-->m=[1 2 3;4 5 6]
m =
1. 2. 3.
4. 5. 6.
วงเล็บใช้เพื่อจัดการองค์ประกอบของเมทริกซ์หรือปรับเปลี่ยนองค์ประกอบ
หมายเหตุ คำสั่งนี้สามารถพิมพ์ภายใต้รูปแบบ m=[1,2,3;4,5,6]
-->m(2,3)
ans =
6.
-->m(2,3)=23
m =
1. 2. 3.
4. 5. 23.
โอเปอร์เรเตอร์ “ : “ ถูกนำมาใช้เพื่อจัดวางแถวทั้งหมดหรือคอร์ลัมน์ทั้งหมดของเมทริกซ์หนึ่งๆ เพื่อมองหาแถวที่ 2 ของเมทริกซ์ m พิมพ์ดังนี้
-->m(2,:)
ans =
4. 5. 23.
และคอร์ลัมน์ที่ 3 ดังนี้
-->m(:,3)
ans =
3.
23.
เพื่อให้ได้มาของการทรานซโพสของเมทริกซ์หนึ่งหรือเว็คเตอร์หนึ่ง ให้ใช้สัญลักษณ์เครื่องหมายคำพูดเดี่ยว “ ' “:
-->m'
ans = 1. 4.
2. 5.
3. 23.
ตัวกระทำ (Operations)
การกระทำ “ * “, “ / “ เป็นการกระทำของเมทริกซ์ เพื่อทำให้ทำให้การกระทำไปตามองค์ประกอบ (element wise operations) เราจำต้องใส่จุดก่อนเครื่องหมายกระทำ: “ .* “, “ ./ “.
-->A=[1,2,3;4,5,6]
A =
1. 2. 3.
4. 5. 6.
-->B=[1;1;2]
B =
1.
1.
2.
-->A*B
ans = การคูณเมทริกซ์ (Matrix multiplication)
9.
21.
-->A*A !--error 10
Inconsistent multiplication. Dimensions are not consistent
-->A.*A
ans = 1. 4. 9. Element wise multiplication
16. 25. 36.
-->2*(A+2)
ans =
6. 8. 10. The operation is performed on each element
12. 14. 16. because 2 is a number
-->A/A กำหนดให้เมทริกซ์ X ที่ซึ่ง X*A = A
ans =
1. 1.518D-16 ผลลัพธ์จริงๆคือ 1. 0
3.795D-15 1. 0 1
สำหรับเหตุผลความถูกต้องในการคำนวณ ผลลัพธ์อาจ
แตกต่างกันเล็กน้อยดขึ้นอยู่กับรุ่นของไซแลบและระบบ
ปฏฺิบัติ การที่ใช้ (ให้ดูความละเอียดในการคำนวณ หนา 29).
-->A./A
ans =
1. 1. 1.
1. 1. 1.
กำหนดให้เมทริกซ์หารตามองค์ประกอบ (divided element wise) ในกรณีของเว็คเตอร์
-->C = 1:4
C = 1. 2. 3. 4.
-->C*C !--error 10 Dimensions are not consistent
Inconsistent multiplication.
-->C.*C
ans =
1. 4. 9. 16.